Basic self-organising network: vector quantiser

The simplest self-organising network (SON) that computes non-linear transformations of data is the vector quantiser (VQ).

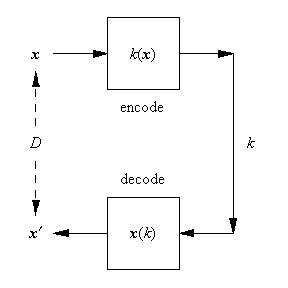
A VQ does two simultaneous jobs:

1. Encoding: take each continuous-valued input vector x and use an encoder k(x) to map it to a discrete-valued code k.
2. Decoding: take each discrete-valued code k and use a decoder x(k) to map it to a continuous-valued input x.

Thus a VQ defines a pair of oppositely directed mappings x → k (i.e. k(x)) and k → x (i.e. x(k)). The "quality" of the encoding may be judged by going once round the encode/decode loop thus x → k → x′, and then comparing the original input vector x with its reconstruction x′. A good VQ will have a small reconstruction error, and to achieve this the two mappings k(x) and x(k) must work together harmoniously.

Now let me explicitly show how to optimise a VQ.

A simple measure of the "goodness" of a VQ is a "Euclidean" objective function D that measures the average squared reconstruction error, which is defined as

D = ∫dx Pr(x)║x - x(k(x))║²

where the various pieces have the following interpretation:

1. x(k(x)) encodes (and then decodes) an input vector x to produce a reconstruction.
2. x - x(k(x)) computes the difference between the original input vector and its reconstruction.
3. ║x - x(k(x))║² computes the squared length of the above difference vector.
4. ∫dx Pr(x)║...║² averages the average of the above squared length over input vectors x with probability density Pr(x).

Minimisation of this objective function with respect to the two mappings k(x) and x(k) optimises the VQ.

By inspection, the optimum k(x) is given by

k(x) = argmin_k║x - x(k)║²

Differentiate D with respect to x(k)

∂D/∂x(k) = -2∫dx Pr(x) δ_k,k(x)(x - x(k))

where δ_k,k(x) is a Kronecker delta. The optimum x(k) satisfies ∂D/∂x(k) = 0 (strictly, this is a necessary but not sufficient condition to locate the global optimum) which is given by

x(k) = (∫dx Pr(x) δ_k,k(x) x) / (∫dx Pr(x) δ_k,k(x))

This pair of coupled non-linear equations for the optimum mappings k(x) and x(k) can be solved iteratively.

1. Randomly initialise the x(k) for k = 1, 2, ..., m where m is the size of the "code book" of x(k) vectors to be optimised.
2. Compute the right hand side of the x(k) = (...) / (...) equation, using the k(x) = ... equation to compute k(x) whenever it is needed. The integrals ∫dx Pr(x) (...) are approximated using a finite-sized set of input vectors x (normally called the "training set").
3. The result for (...) / (...) from step 2 above will in general not be the same as the previously assigned values for the x(k). The resolution of this is to overwrite the previous values of the x(k) with the newly computed (...) / (...) from step 2 above, and to iterate this process.
4. When the x(k) have settled down so that successive iterations give (approximately) the same result the optimisation has converged to a minimum of the objective function. Note that this is guaranteed to be a local minimum, but not guaranteed to be a global minimum.

Why is a VQ a SON?

The encoder and decoder pair of mappings k(x) and x(k) bidirectionally connect two spaces (x-space and k-space) thus x ↔ k. The encode/decode loop x → k → x′ contains all the places that k appears, i.e. mapping k(x), k-space, and mapping x(k). The structure of this encode/decode loop is determined entirely by the minimisation of an objective function, and the term "self-organisation" is used to describe the optimisation process that creates the loop x → k → x′. As a side effect of the creation of this encode/decode loop a new space (i.e. k-space) is created that is able to "represent" states in x-space.

This creation of mappings to and from new "representation" spaces is a defining feature of SONs, and the VQ is the simplest example using non-linear mappings that I know of. If the discrete-valued k is replaced by a continuous-valued k, or more generally a vector k, then using a Euclidean objective function the optimum mappings k(x) and x(k) are linear (this is "principal components analysis", or PCA). Note that networks of linear mappings can build only linear mappings, whereas networks of non-linear mappings can build all mappings. It is very convenient that merely using a discrete-valued (rather than a continuous-valued) k or k leads to the useful non-linearity found in a VQ.

This use of discrete-valued quantities turns out to absolutely crucial for building a generalised theory of SONs. I will repeatedly return to this theme in the future.