This posting is a brief overview of my recent paper entitled "Discrete network dynamics. Part 1: Operator theory", which can be found in arXiv at
cs.NE/0511027.
The basic idea is that an MCMC simulation (see a description of MCMC algorithms in a previous posting of mine
here) of a joint probability Pr(
x), where
x is the joint state of an
N-dimensional system (e.g.
xi is the state of the
ith node of an
N-node network), generates a sequence of
x's (i.e.
x(1),
x(2), ... ,
x(
t), ...) that are sampled from Pr(
x).
x(
t+1) is generated from
x(
t) by an operation that holds some of the components of
x(
t) fixed, whilst stochastically updating the rest of the components of
x(
t). The MCMC update operation is chosen so that if Pr(
x(
t)) has the correct joint probability then so also does Pr(
x(
t+1)). This was discussed in detail
here.
The MCMC update operation is particularly simple if the state of only
one of the nodes of the network is updated at a time, so that
x(
t+1) differs from
x(
t) in only
one of its vector components. Let us assume that it is the
ith component that is updated, then MCMC update operation consists of two simpler operations:
- Erase the state xi. This is an unconditional erase operation, in which the state is erased with no memory of what it used to be.
- Randomly rewrite the state xi. This is a conditional rewrite operation, in which the state is drawn from the conditional probability Pr(xi│x\xi).
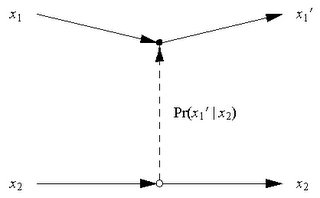
The diagram shows an MCMC update in a visually intuitive way for a 2-node network (i.e. N=2). Node 1 is at the top of the diagram, node 2 is at the bottom of the diagram, and time reads from left to right across the diagram. The initial state x1 of node 1 is changed to final state x1´ by the influence of the state x2 of node 2 (which is itself unchanged in going from initial to final state). The solid lines from left to right indicate the evolution of the states of nodes 1 and 2. The vertical dashed line indicates the influence of the state of node 2 on the state of node 1, and the probability of the final state of node 1 is indicated as Pr(x1´│x2), which is memoryless because it does not depend on x1.
The above diagram is a Feynman-like diagram describing the annihilation of the state of node 1, and then subsequent creation of a new state for node 1, and the "amplitude" for this process is actually a probability given by Pr(x1´│x2).
This identification allows the MCMC update operator to be written as
Ha ≡ ∑i ai† (∑jaj) (∑kPr(i│k) bk†bk)
where ai† is the creation operator for state i at node 1, bk† is the creation operator for state k at node 2, bk†bk is the number operator for state k at node 2, ∑kPr(i│k) bk†bk is the operator for computing the conditional probability factor that weights the MCMC update, and ∑jaj unconditionally annihilates the state at node 1.
Application of the MCMC update operator Ha automatically generates the correct probability-weighted ensemble of possible next states of the 2-node network in which the state of node 1 is updated. The full MCMC update operator is the sum of Ha+Hb, where Hb is obtained from Ha by interchanging the "a" and "b" operators (and appropriately changing the conditional probability factor). The Feynman-like diagram version of Ha+Hb is thus a sum of two diagrams as shown below.

The MCMC update operator correctly implements the 2-step MCMC update procedure described earlier. Each node of the network has a state with occupancy 1 that is erased (i.e. annhilated) during step 1 of the MCMC update to become the "vacuum" state with occupancy 0, and the state is rewritten (i.e. created) during step 2 of the MCMC update to become a state with occupancy 1 again. This update process is memoryless because its intermediate state is the "vacuum".
However, the MCMC update operator goes beyond the standard MCMC updates, because it can also be applied to initial states that have an occupancy of 2 or more. The algebra of the creation and annihilation operators automatically does this generalisation for you, and thus defines a unique generalisation of the MCMC algorithm for multiply occupied states of the network nodes.
The above discussion has focussed on a network with only 2 nodes. The generalisation to an N-node network is straightforward when the probability Pr(x) of the joint state of the network is expanded using the Hammersley-Clifford expansion, as is shown in my paper.
The structure of this MCMC algorithm is similar to a quantum field theory of bosons:
- Each state of node i of the network can have a variable occupancy, which corresponds to each state of bosons of type i having a variable occupancy.
- An MCMC update causes the multiply occupied state of node i of the network to change by using the neighbouring nodes to influence the hopping of an occupant from one state of node i to another state of node i, which corresponds to a boson of type i scattering from one state to another under the influence of bosons of various other types.
This completes the reformulation of MCMC algorithms using the language of creation and annihilation operators, and opens up a large number of possible lines of enquiry.
One particularly interesting consequence of multiple occupancy MCMC algorithms is self-organising networks, in which the state space of a multiply occupied network node can split into 2 or more smaller state spaces, each of which inherits some of the original node's multiple occupants, so that overall the original node splits into several daughter nodes. I will be saying much more about this later.


